
Adding and Subtracting Surds GCSE Steps, Examples & Worksheet
When you add and subtract surds, the numbers inside the square root must be the same. You add/ subtract the number outside the square root. e.g. 2√5 + 7√5 = 9√5, however 2√5 + 7√3 cannot be added. when you multiply and divide surds there is a different set of rules. If the 2 numbers inside the surd are the same, this creates a whole.

Adding and subtracting surds YouTube
Learning surd is fun, Watch this lesson and learn how to add and subtract surds. In the process you will be introduced to "like surds". Watch and learn about.

4 Addition of surds YouTube
Adding & Subtracting Surds | Numbers | Maths | FuseSchoolIn this video we are going to have a quick look at adding and subtracting surds. You should already.
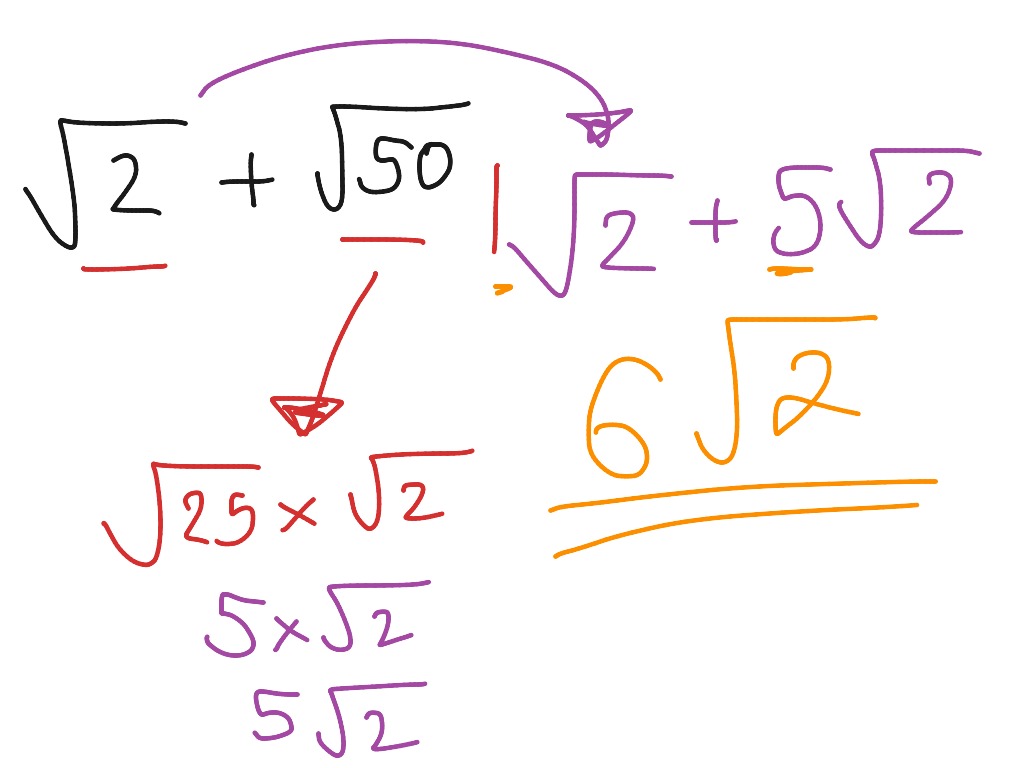
Adding surds Math, Algebra, Simplifying Expressions, Adding Surds ShowMe
Adding Surds Video Addition and Subtraction of Surds Video tutorial. Videos; addition surds; subtraction surds; Post navigation. Previous Multiplying a Matrix by a Scalar Video. Next Non-UK Order. GCSE Revision Cards. 5-a-day Workbooks. Primary Study Cards. Search for: Contact us.

Adding Surds Video Corbettmaths
How to add or subtract two or more surds. The addition and subtraction of surds are the basic two operations on surds. The below steps need to be checked while adding two or more surds. Step 1: First look into the sum (or difference) and check whether the surds involved in the sum (or difference) are in the simplest forms or not.

How to add and subtract surdsAdding and subtracting surds worksheetSurds addition and
This video explains how to add and subtract surds. It is ideal for students studying for AS Maths, Level 2 Further Maths or even keen GCSE students!

Adding and Subtracting Surds 5 YouTube
Follow the following steps to find the addition and subtraction of two or more surds: Step I: Convert each surd in its simplest mixed form. Step II: Then find the sum or difference of rational co-efficient of like surds. Step III: Finally, to get the required sum or difference of like surds multiply the result obtained in step II by the surd.

How to Simplify Surds
Surds. When we can't simplify a number to remove a square root (or cube root etc) then it is a surd. Example: √ 2 (square root of 2) can't be simplified further so it is a surd. Example: √ 4 (square root of 4) can be simplified (to 2), so it is not a surd! Have a look at some more examples: Number. Simplified.

Addition and Subtraction of Surds YouTube
This video demonstrates how to add and subtract surds when they are the same type or if they need to be simplified first. For more Math content check out www.

How to Simplify Surds
Learn about and revise surds, including how to add, subtract, multiply and divide them, with with GCSE Bitesize Maths.

MEDIAN Don Steward mathematics teaching introducing surds
What is adding and subtracting surds? Adding and subtracting surds is where we can add or subtract surds when the numbers underneath the root symbols (the radicands) are the same; these are called 'like surds'. This is similar to collecting like terms in algebra: E.g. a + a + 2a simplifies to 4a. So when we do a similar thing with surds: E.g.
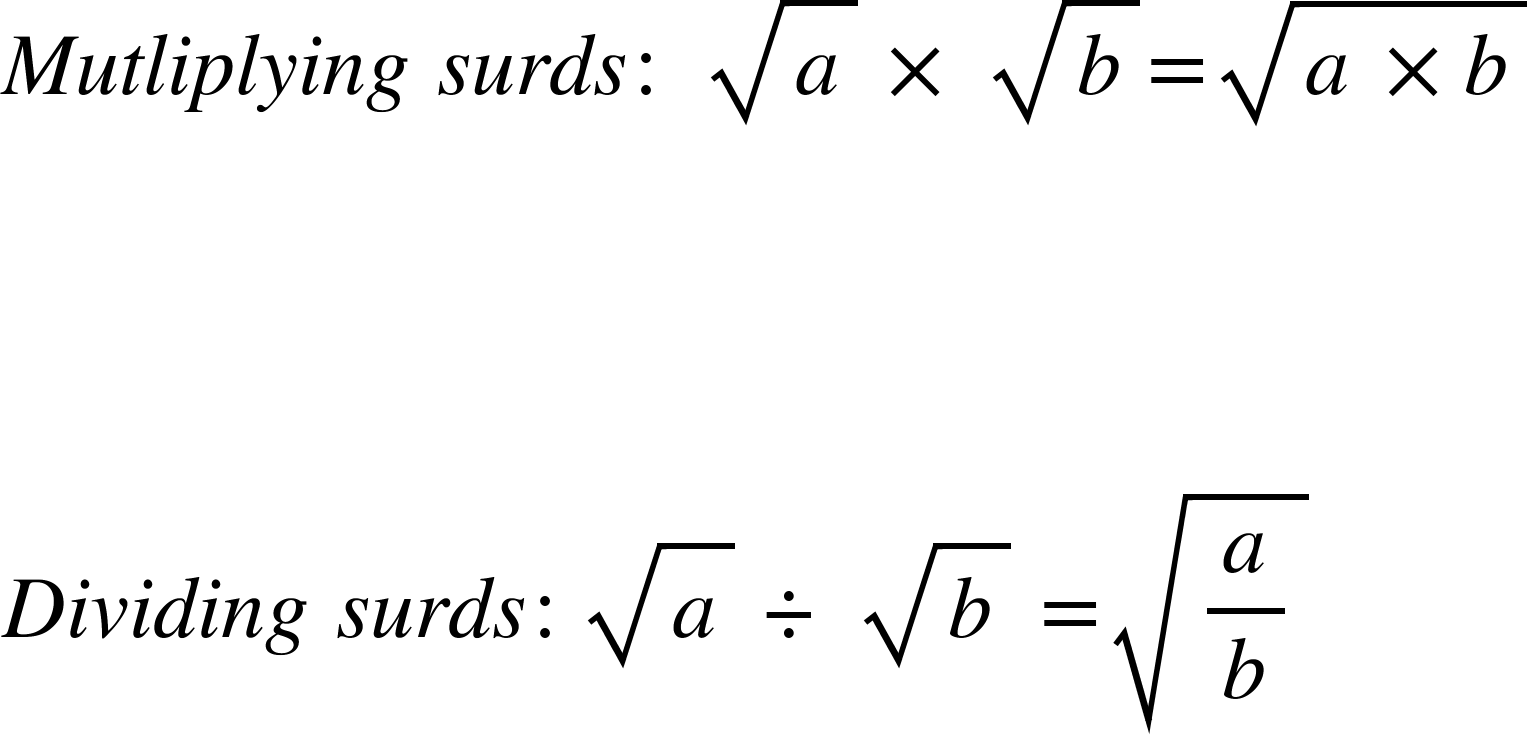
Surds GCSE Mathematics Edexcel Revision Study Rocket
Corbettmaths - This video explains what a surd is, how to simplify, multiply or divide them. It explains the rules of surds.

Surds 2 Arithmetic of surds Adding and Subtracting YouTube
Corbettmaths - This video shows how to add surds and the importance of simplifying them beforehand.

Adding Surds Corbettmaths YouTube
The rule for adding and subtracting surds is that the numbers inside the square roots close square root The square root of a number is a number which, when multiplied by itself, gives the original.
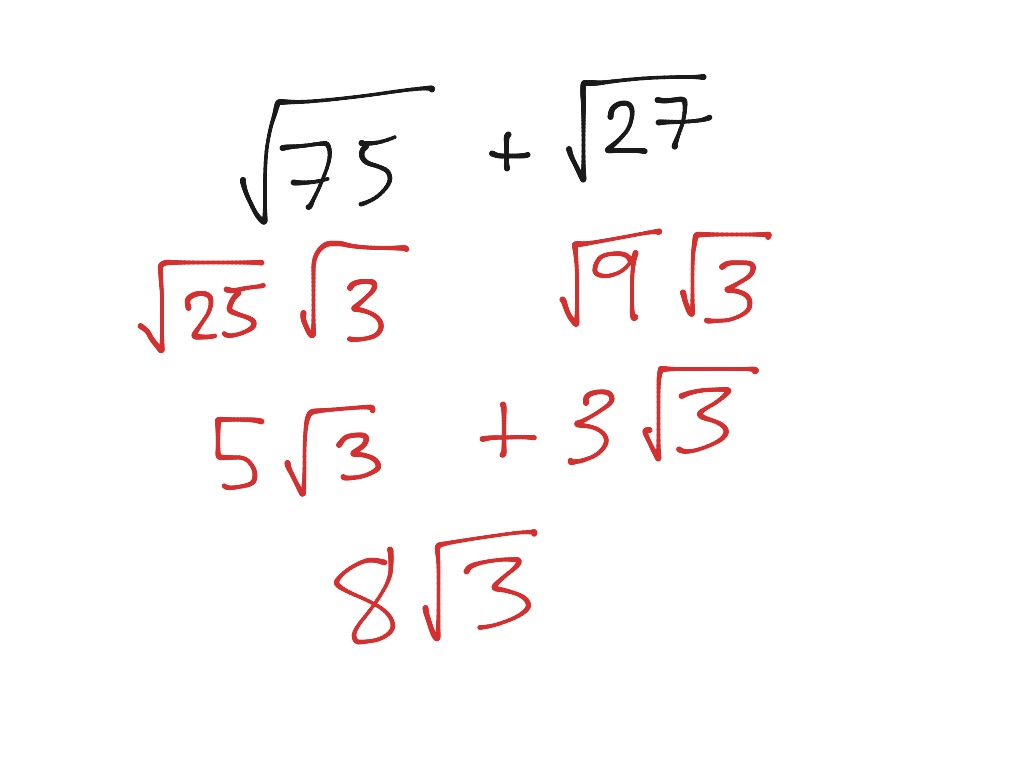
Surds for Eliza Math, Arithmetic, Adding Surds ShowMe
Learn about and revise surds, including how to add, subtract, multiply and divide them with GCSE Bitesize AQA Maths.

Surds / Radicals the basics adding and subtracting made easy YouTube
Adding and subtracting surds are simple- however we need the numbers being square rooted (or cube rooted etc) to be the same. 4√7 - 2√7 = 2√7. 5√2 + 8√2 = 13√2. Note: 5√2 + 3√3 cannot be manipulated because the surds are different (one is √2 and one is √3). However, if the number in the square root sign isn't prime, we might.