
Euclidean & NonEuclidean Geometries Development and History by Marvin Jay Greenberg
Euclidean and non-Euclidean geometries by Greenberg, Marvin J. Publication date 2008 Topics Geometry, Geometry, Non-Euclidean, Geometry -- History, Geometry, Non-Euclidean -- History Publisher New York : W.H. Freeman Collection printdisabled; internetarchivebooks Contributor Internet Archive

Non euclidean geometry Fun math, Math patterns, Math tutorials
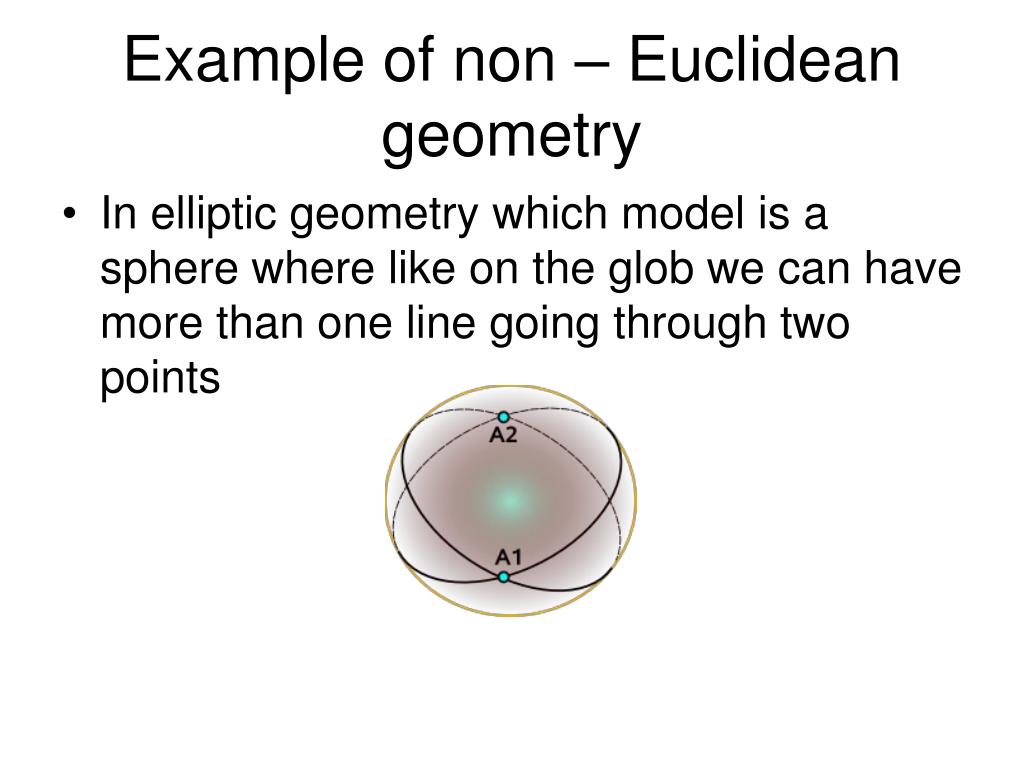
The negatively curved non-Euclidean geometry is called hyperbolic geometry. Euclidean geometry in this classification is parabolic geometry, though the name is less-often used. Spherical geometry is called elliptic geometry, but the space of elliptic geometry is really has points = antipodal pairs on the sphere. With this idea, two lines really
PPT Geometry Points, Lines, Planes, and Angles PowerPoint Presentation ID3809793
This is the definitive presentation of the history, development and philosophical significance of non-Euclidean geometry as well as of the rigorous foundations for it and for elementary Euclidean geometry, essentially according to Hilbert. Appropriate for liberal arts students, prospective high school teachers, math. majors, and even bright.

what does Non Euclidean geometry mean?? YouTube
There are two main types of non-Euclidean geometries, spherical (or elliptical) and hyperbolic. They can be viewed either as opposite or complimentary, depending on the aspect we consider. I will point out some of the theoretical aspects in the final sections of these presentation. Hyperbolic geometry and handcrafts

NonEuclidean Geometry YouTube
Euclidean and Non-Euclidean Geometries. : Marvin J. Greenberg. W. H. Freeman, Aug 15, 2008 - Mathematics - 512 pages. This is the definitive presentation of the history, development and philosophical significance of non-Euclidean geometry as well as of the rigorous foundations for it and for elementary Euclidean geometry, essentially according.

NonEuclidean geometry YouTube
Professor of mathematics, Cornell University, Ithaca, N.Y. Author of Differential Geometry: A Geometric Introduction and Experiencing Geometry in Euclidean, Spherical, and Hyperbolic Spaces. David W. Henderson, Daina Taimina

Euclidean and NonEuclidean Geometry
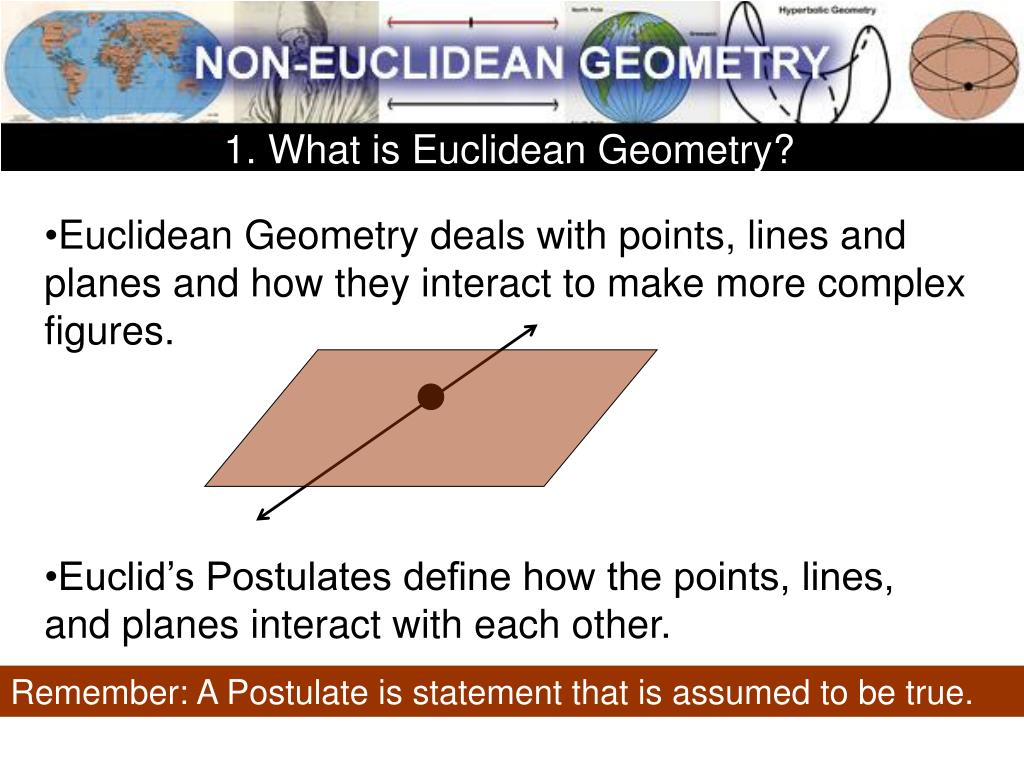
non-Euclidean. non-Eu·clid·e·an / ˌnän yoōˈklidēən / • adj. Geom. denying or going beyond Euclidean principles in geometry, esp. in contravening the postulate that only one line through a given point can be parallel to a given line. non-Euclidean geometry, branch of geometry [1] in which the fifth postulate of Euclidean geometry.

NonEuclidean geometry and games. The term “nonEuclidean” is often used… by Zeno Rogue Medium
Abstract We intend to construct these geometries using a slightly modified Hilbert's axioms system in the same way as it is done in [7-10]. An interesting thing is related to the fact that it exists a common part for Euclidean and Non-Euclidean Geometry, the so called Absolute Geometry.
PPT Mr. Young’s Geometry Classes, Spring 2005 PowerPoint Presentation ID1274559
The "flat" geometry of everyday intuition is called Euclidean geometry (or parabolic geometry), and the non-Euclidean geometries are called hyperbolic geometry (or Lobachevsky-Bolyai-Gauss geometry) and elliptic geometry (or Riemannian geometry). Spherical geometry is a non-Euclidean two-dimensional geometry.

Euclidean and NonEuclidean Geometry An Analytic Approach by Patrick J. Ryan
In the literal sense — all geometric systems distinct from Euclidean geometry; usually, however, the term "non-Euclidean geometries" is reserved for geometric systems (distinct from Euclidean geometry) in which the motion of figures is defined, and this with the same degree of freedom as in Euclidean geometry.

7 euclidean&non euclidean geometry
Geometry Projecting a sphere to a plane Outline History ( Timeline) Branches Euclidean Non-Euclidean Elliptic Spherical Hyperbolic Non-Archimedean geometry Projective Affine Synthetic Analytic Algebraic Arithmetic Diophantine Differential Riemannian Symplectic Discrete differential Complex Finite Discrete/Combinatorial Digital Convex Computational

PPT NonEuclidean geometry and consistency PowerPoint Presentation, free download ID2683826
This is the definitive presentation of the history, development and philosophical significance of non-Euclidean geometry as well as of the rigorous foundations for it and for elementary Euclidean geometry, essentially according to Hilbert. Appropriate for liberal arts students, prospective high school teachers, math. majors, and even bright.

Euclidean and NonEuclidean Geometries Development and History by Marvin Jay Gr 9780716799481
This book gives a rigorous treatment of the fundamentals of plane geometry: Euclidean, spherical, elliptical and hyperbolic. The primary purpose is to acquaint the reader with the classical results of plane Euclidean and nonEuclidean geometry, congruence theorems, concurrence theorems, classification of isometries, angle addition and trigonometrical formulae.

Euclidean and NonEuclidean geometries Foldable (open). Euclidean geometry, Geometry lessons
Chapter 1 Introduction Yes, there are hundreds of Geometry textbooks written and published. What is the reason for this one then? The present lecture notes is written to accompany the course math551, Euclidean and Non- Euclidean Geometries, at UNC Chapel Hill in the early 2000s.

NonEuclidean geometry YouTube
Euclidean and non-euclidean geometry Until the 19th century Euclidean geometry was the only known system of geometry concerned with measurement and the concepts of congruence, parallelism and perpendicularity. Then, early in that century, a new system dealing with the same concepts was discovered.

EUCLIDEAN AND NONEUCLIDEAN GEOMETRIES DEVELOPMENT AND HISTORY written by Greenberg, Marvin Jay
It is called "Non-Euclidean" because it is different from Euclidean geometry, which was developed by an ancient Greek mathematician called Euclid. Some History… The birth of non-Euclidean geometry was REALLY a big deal. It was truly a ground-shaking event, not only in the history of mathematics and but also in philosophy.